Solstick: Example Result

We can estimate the size of the Earth by seeing how far away you are from somewhere nearer the equator where the Sun was directly overhead at the time you took your measurements. You can see how this works in detail here.
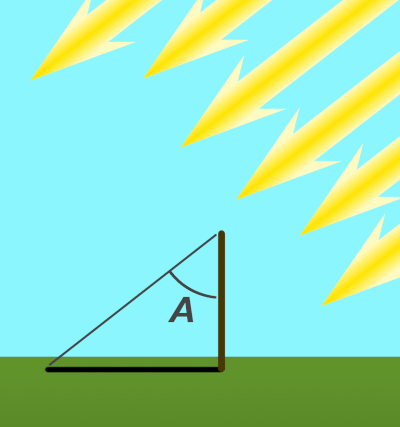
Your shadow of 56 cm from a stick 100 cm tall made an angle of 29o to the stick (the angle A in the diagram).
This means that the distance between where you are and where the Sun was exactly overhead is 8% of the way around the globe.
We also know from your postcode that if you wanted to go to where the Sun was overhead, you would have to walk south for 3340 km.
That means that all the way around the world - the circumference - would be 41500 km and the diameter of the Earth would be 13200 km
Since the actual circumference of the Earth is 40000 km your estimate of 41500 km is really very close.
If you want to see exactly how we worked this out, the full working is below.
Using lots of results
Whenever a scientist makes a measurement, there are always things that she cannot get exactly right, so the final number is never perfect. We call that small imperfection an error and all measurements have them.
Your measurement will also have an "error" - maybe the ground was not exactly flat, or the shadow was bit too fuzzy to see exactly where the end was and so on. You cannot do anything about this, so your answer will never be perfect, even if it is pretty good! However, if your number is a bit too small, somebody else might have an answer that is a bit too large. So, if we get lots of results and average them, all the errors will start to cancel out, and the final value will be much better than any single answer could possibly be.
This is why we want to collect as many measurements as possible. If you want to see what the final result is, come back in a few days when we have all the measurements in!
How we calculated your answer
With any scientific result it is important to know how the answer was worked out, so here is a step-by-step description of the working to get your estimate of the size of the Earth
In order to get an answer, we actually need not one shadow but two - both measured at the same time, and one much further south than the other like this:
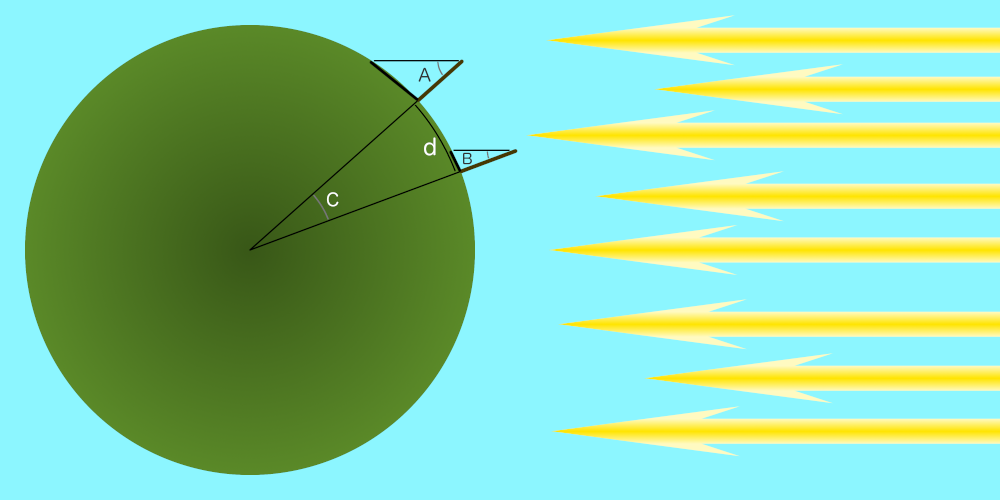
You cannot do this with just your shadow but, if you know what a shadow would be like at a suitable place and time, you do not need to actually measure it. Fortunately we know (as did ancient astronomers like Eratosthenes) that on the summer Solstice, the Sun will be exactly overhead in the middle of the day anywhere along the Tropic of Cancer (which is an imaginary line which runs round the world a bit north of the Equator).
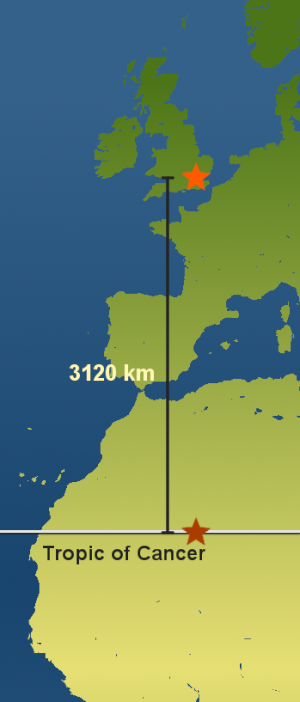
to the Tropic of Cancer
So, as you have taken your measurement near to the Solstice (which is the 21st June 2023) and around the middle of the day (1PM British Summer Time), we can use an imaginary second stick due south of the UK on the Tropic of Cancer - right in the middle of the Algerian desert
In Eratothenes' day he had to rely on people keeping records of their travels over many weeks to work out the distance between places, but we are much luckier as explorers and cartographers have been making maps for hundreds of years, so we can just use them to find distances. For this experiment we are using two maps: a small scale map to find the distance from one place in the UK to the Tropic of Cancer (we chose the Greenwich Observatory in London) and a larger scale map of the UK to find out how far north or south you are from Greenwich. Using the two together, we can work out how far north you are from the Tropic.
Step by Step
- Using your postcode and the large scale map of the UK we know that you are about 220 km north of the Greenwich Observatory.
- So your total distance from the Tropic of Cancer (d) is 3120 + 220 = 3340 km.
- Next we need to know the angle of your shadow A. Since we have a right-angled triangle, then:
tan(A) = shadow length / stick height
tan(A) = 56 / 100
So A = tan-1(56 / 100) = 29o. - Since the imaginary stick on the Tropic of Cancer has the Sun directly overhead, the angle B is zero, so angle C is the same as angle A (29o).
- 29o is 8% of 360o, so the distance between you and the Tropic of Cancer is 8% of the way around the globe.
- So the total circumference of the Earth from your measurements is:
Circumference = d x 360 / A
= 3340 x 360 / 29
= 41462 km. - Finally, rounding to the nearest 100km gives your estimate of the circumference of the Earth as 41500 km.

