Wien's Law
Stars absorb and emit light. This light covers a wide range of wavelengths, known as a spectrum. Remember when we talk about light, this includes the entire electromagnetic spectrum.
We can measure the amount of light energy that an object emits. This is often referred to as the intensity of the light. Objects emit different wavelengths at different intensities. The wavelength that corresponds to the highest intensity is called λmax.
Wein's Law shows the relationship between an object's temperature and the wavelength at which it emits the most light. We can use the λmax of a star and Wein's Law to work out the star's surface temperature.
Wein's Law states that Temperature (T) = b / λmax. Where b = Wien's displacement constant, equal to 2.897771955...×10−3 m K.
This formula is true for a blackbody. A blackbody is an object that is perfect at absorbing and emitting all radiation. These theoretical objects have, so far, not been found to exist. However, stars are very good emitters of all radiation, so we can consider them to be black bodies. We can do the same for planets and black holes.
Let's work through an example. We'll use the Sun. The λmax of the Sun is about 500 nm (5 x 10-7 m).
T = b / λmax
T = 2.898 × 10-3 / 5 x 10-7
T = 5800 K
So the Sun's surface temperature is about 5800 K.
You can see from the formula that as the temperature increases, λmax will decrease. Stars of 12,000 K and hotter tend to have λmax at UV wavelengths. Stars at around 8000 K have λmax in the blue part of the optical spectrum. So the colour of a star also gives us information about its temperature. Redder stars are cooler and bluer stars are hotter.
By using a telescope with colour filters, we can work out the colour of a star. We use the apparent magnitude of the star seen through 2 different filters to quantify the colour.
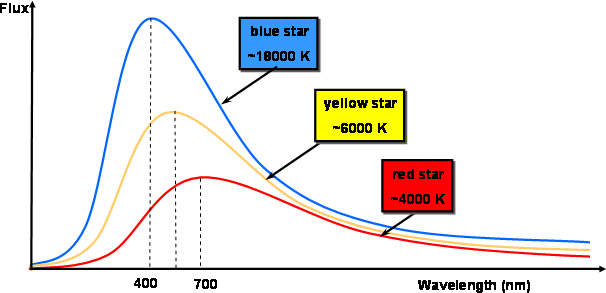
The x-axis represents the light's wavelength from violet to red
The y-axis represents the amount of light at a given wavelength).
Credit: Swinburne University

